WHAT IS SOFTMAX
Softmax regression always as one module in a deep learning network, and most likely to be the last module, the output module. What is it? It is a generalized version of logistic regression. Just like logistic regression, it belongs to supervised learning, and the superiority is, the class label y can be more than two values. Which means, compare to logistic regression, the amount of class will not be restricted to two. However, someone may recall that we can use “1 VS others” method to deal with multi-class problems, I hold this question for a while and let’s see formulae of softmax regression.
First let’s see its hypothesis hθ(x)

in which, k means given a test input x, the output y can be any value in set [1, 2, … , k], we want to estimate the probability of the class label taking on each of the k different possible values. So the hθ(x) will be a k dimensional vector.
However, when the products 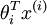 are large, the exponential function
are large, the exponential function 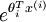 will become very very large and possibly overflow. To prevent overflow, we can simply subtract some large constant value from each of the
will become very very large and possibly overflow. To prevent overflow, we can simply subtract some large constant value from each of the 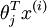 terms before computing the exponential. In practice, for each example, you can use the maximum of the
terms before computing the exponential. In practice, for each example, you can use the maximum of the 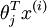 terms as the constant.
terms as the constant.

And followed by cost function and gradient:



In which, the λ part is called weight decay, which penalizes large values of the parameters. After implementing these part, we can use gradient descent or other advanced methods to get optimal θ by minimizing J(θ) with respect to θ.
SOURCE CODE
010 | #define MAX_ITER 100000 |
018 | colvec vec2colvec(vector<double>& vec){ |
019 | int length = vec.size(); |
021 | for(int i=0; i<length; i++){ |
027 | rowvec vec2rowvec(vector<double>& vec){ |
028 | colvec A = vec2colvec(vec); |
032 | mat vec2mat(vector<vector<double> >&vec){ |
033 | int cols = vec.size(); |
034 | int rows = vec[0].size(); |
036 | for(int i = 0; i<rows; i++){ |
037 | for(int j=0; j<cols; j++){ |
044 | void update_CostFunction_and_Gradient(mat x, rowvec y, mat weightsMatrix, double lambda){ |
046 | int nsamples = x.n_cols; |
047 | int nfeatures = x.n_rows; |
049 | mat theta(weightsMatrix); |
051 | mat temp = repmat(max(M, 0), nclasses, 1); |
054 | temp = repmat(sum(M, 0), nclasses, 1); |
057 | mat groundTruth = zeros<mat> (nclasses, nsamples); |
058 | for(int i=0; i<y.size(); i++){ |
059 | groundTruth(y(i), i) = 1; |
061 | temp = groundTruth % (arma::log(M)); |
062 | cost = -accu(temp) / nsamples; |
063 | cost += accu(arma::pow(theta, 2)) * lambda / 2; |
066 | temp = groundTruth - M; |
068 | grad = - temp / nsamples; |
069 | grad += lambda * theta; |
072 | rowvec calculateY(mat x, mat weightsMatrix){ |
074 | mat theta(weightsMatrix); |
076 | mat temp = repmat(max(M, 0), nclasses, 1); |
079 | temp = repmat(sum(M, 0), nclasses, 1); |
082 | rowvec result = zeros<rowvec>(M.n_cols); |
083 | for(int i=0; i<M.n_cols; i++){ |
084 | int maxele = INT_MIN; |
086 | for(int j=0; j<M.n_rows; j++){ |
087 | if(M(j, i) > maxele){ |
097 | void softmax(vector<vector<double> >&vecX, vector<double> &vecY, vector<vector<double> >& testX, vector<double>& testY){ |
099 | int nsamples = vecX.size(); |
100 | int nfeatures = vecX[0].size(); |
102 | rowvec y = vec2rowvec(vecY); |
103 | mat x = vec2mat(vecX); |
105 | double init_epsilon = 0.12; |
106 | mat weightsMatrix = randu<mat>(nclasses, nfeatures); |
107 | weightsMatrix = weightsMatrix * (2 * init_epsilon) - init_epsilon; |
108 | grad = zeros<mat>(nclasses, nfeatures); |
134 | double lastcost = 0.0; |
135 | while(converge < MAX_ITER){ |
136 | update_CostFunction_and_Gradient(x, y, weightsMatrix, lambda); |
137 | weightsMatrix -= lrate * grad; |
139 | cout<<"learning step: "<<converge<<", Cost function value = "<<cost<<endl; |
140 | if(fabs((cost - lastcost) ) <= 5e-6 && converge > 0) break; |
144 | cout<<"############result#############"<<endl; |
146 | rowvec yT = vec2rowvec(testY); |
147 | mat xT = vec2mat(testX); |
148 | rowvec result = calculateY(xT, weightsMatrix); |
149 | rowvec error = yT - result; |
150 | int correct = error.size(); |
151 | for(int i=0; i<error.size(); i++){ |
152 | if(error(i) != 0) --correct; |
154 | cout<<"correct: "<<correct<<", total: "<<error.size()<<", accuracy: "<<double(correct) / (double)(error.size())<<endl; |
158 | int main(int argc, char** argv) |
162 | FILE *streamX, *streamY; |
163 | streamX = fopen("trainX.txt", "r"); |
165 | vector<vector<double> > vecX; |
169 | if(fscanf(streamX, "%lf", &tpdouble)==EOF) break; |
170 | if(counter / numofX >= vecX.size()){ |
171 | vector<double> tpvec; |
172 | vecX.push_back(tpvec); |
174 | vecX[counter / numofX].push_back(tpdouble); |
179 | cout<<vecX.size()<<", "<<vecX[0].size()<<endl; |
182 | streamY = fopen("trainY.txt", "r"); |
185 | if(fscanf(streamY, "%lf", &tpdouble)==EOF) break; |
186 | vecY.push_back(tpdouble); |
190 | for(int i = 1; i<vecX.size(); i++){ |
191 | if(vecX[i].size() != vecX[i - 1].size()) return 0; |
193 | if(vecX.size() != vecY.size()) return 0; |
195 | streamX = fopen("testX.txt", "r"); |
196 | vector<vector<double> > vecTX; |
199 | if(fscanf(streamX, "%lf", &tpdouble)==EOF) break; |
200 | if(counter / numofX >= vecTX.size()){ |
201 | vector<double> tpvec; |
202 | vecTX.push_back(tpvec); |
204 | vecTX[counter / numofX].push_back(tpdouble); |
209 | streamY = fopen("testY.txt", "r"); |
210 | vector<double> vecTY; |
212 | if(fscanf(streamY, "%lf", &tpdouble)==EOF) break; |
213 | vecTY.push_back(tpdouble); |
218 | softmax(vecX, vecY, vecTX, vecTY); |
220 | cout<<"Training used time: "<<((double)(end - start)) / CLOCKS_PER_SEC<<" second"<<endl; |
TEST RESULT
I used Wisconsin Breast Cancer dataset, which has 284 training samples and 284 test samples, there are 30 features in each sample, you can download the dataset here:
trainX.txt trainY.txt
testX.txt testY.txt
Here’s the result.

You can see the speed is very fast, that is because I used Vectorization method during the training process, which means minimize the amount of loop I use. Check my update_CostFunction_and_Gradient function, you will see the trick.
SOFTMAX VS MULTI-BINARY CLASSIFIERS
Now let’s retrieve back to the above question about softmax VS multi-binary classifiers. As Prof. Andrew Ng says, which algorithm to use depend on whether the classes are mutually exclusive, which means, whether the classes are mixed. For example:
- Case 1. classes are [1, 2, 3, 4, 5, 6]
- Case 2. classes are [1, 2, 3, odd, even, positive]
For case 1, Softmax regression classifier would be fine, in the second case, use multi-logistic regression.

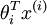 are large, the exponential function
are large, the exponential function 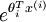 will become very very large and possibly overflow. To prevent overflow, we can simply subtract some large constant value from each of the
will become very very large and possibly overflow. To prevent overflow, we can simply subtract some large constant value from each of the 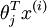 terms before computing the exponential. In practice, for each example, you can use the maximum of the
terms before computing the exponential. In practice, for each example, you can use the maximum of the 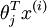 terms as the constant.
terms as the constant.![]()






